Nudged Elastic Band
Computation of a reaction path: the NEB method
Some physical phenomena can be described simply as the crossing of an energy barrier. It is the case with the migration of an atom (or vacancy), or the elementary step of a dislocation moving from a stable position (at the bottom of its Peierls valley) to the next. In this type of problem the initial and final states of the system are known, and one tries to determine what are the intermediate steps and the energy barrier associated with the process. The Nudged Elastic Band (NEB) method is well suited to solve this kind of problem.
Construction of intermediate configurations
Since only the initial and final states are known, one has to start with a guess of the intermediate states. The most simple solution is to use linear interpolation: one assumes that during the reaction atoms move from their initial to final position in a straight line. This approach is the most commonly used to construct configurations before a NEB calculation.

Fig.1 - An example of physical process involving an energy barrier: the migration of an atom.
The intermediate configurations can easily be constructed by interpolation between the initial state (left) and the final state (right).
However, in some cases the linear interpolation may be unsuitable, for instance if two atoms are located very close to one another in an intermediate configuration, or if part of the system is rotated. Also, when a straight dislocation moves from one stable position to the next, linear interpolation is completely unable to produce intermediate states where the dislocation contains kink pairs. In general, as soon as the path of atoms deviates significantly from a straight line, linear interpolation is poorly suited. It is then up to the user to construct realistic intermediate states.
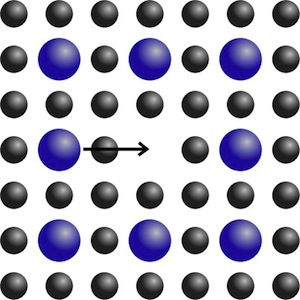
Fig.2 - An example where linear interpolation is not suited: the blue atom would occupy the same position as another atom, which is physically impossible. One has to use another scheme to construct intermediate configurations.
One practical way to construct intermediate configurations without making any assumption about the reaction path is to use molecular dynamics (MD). Starting from the initial step, one can perform a molecular dynamics simulation until the system ends up in a configuration close to the desired final state. The intermediate states produced during the MD run are naturally close to the minimum energy path. This approach is however difficult to apply if the process studied is a rare event. Other algorithms have been proposed to construct intermediate states [1].
Optimisation of the reaction path: the NEB method
The initial path, built by linear interpolation (or another method) is often different from the minimum energy path (Fig.3). It has to be optimized. However the simple relaxation of intermediate configurations is unappropriate: these unstable configurations would end up in the closest stable state, i.e. the initial or final state, which is not desired.
In the Nudged Elastic Band (NEB) method [2], the intermediate configurations are bonded together with springs, so that they are always constrained to remain between the configurations that precedes and follow them. Then the configurations act as an elastic chain.
Of the true force that applies to atoms, only the component normal to the reaction path is used (Fr⊥). Along the reaction path it is the force due to the springs that applies to atoms (Fk//). The NEB calculation stops when the sum of these forces is zero (or drops below a given convergence criterion).
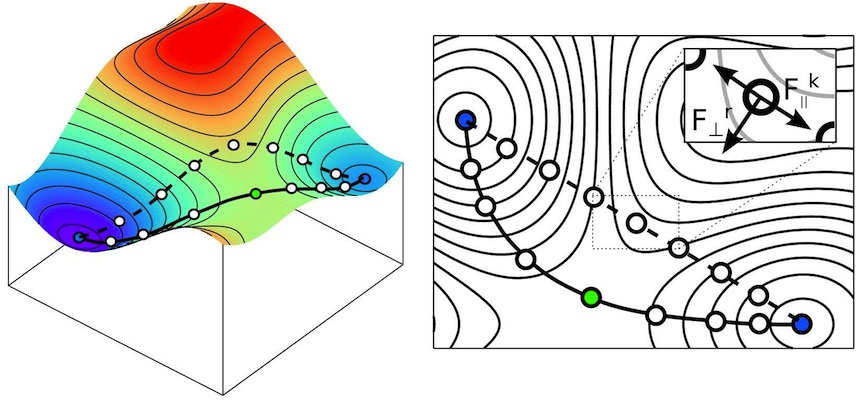
Fig.3 - Principle of the NEB method. The dashed line shows the path corresponding to the initial guess for the intermediate state. After applying the NEB method, the configurations lie along the minimum energy path (continuous line). The green dot corresponds to the transition state (saddle point).
The saddle point configuration: the Climbing NEB
After the optimization of the energy path there is no guarantee that one of the intermediate configuration is exactly at the saddle point. The calculation can then be refined with the climbing NEB method [3]. The configuration of highest energy is moved along the reaction path so as to maximize its energy. Its final configuration is the transition state, or saddle-point configuration.
References
[1] S. Smidstrup et al., J. Chem. Phys. 140 (2014) 214106.
[2] H. Jonsson et al., Classical and Quantum Dynamics in Condensed Phase Simulations, edited by B. J. Berne, G. Ciccotti, and D. F. Coker (World Scientific, Singapore, 1998), p. 385.
[3] G. Henkelman et al., J. Chem. Phys. 113 (2000) 9901.

