This article describes the dislocation microstructure of an olivine single crystal deformed at 1090 °C. Characterizations have been performed by transmission electron tomography. The dislocation population is complex, composed of [001] and [100] dislocations with 3D configurations.

 

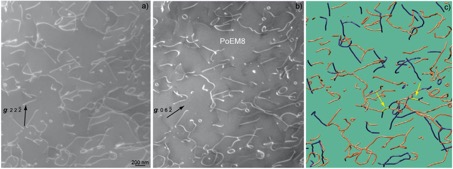
Figure 1: Typical PoEM8 microstructure: (a) WBDF micrograph obtained with the 2 2 -2 diffraction vector ([1 0 0] and [0 0 1] dislocations are in contrast); (b) WBDF micrograph obtained with g = 0 6 -2 on the same region as (a) (only [0 0 1] dislocations are in contrast); (c) Corresponding 3D reconstruction ([1 0 0], [0 0 1] and [1 0 -1] dislocations are shown in blue, orange and yellow colours, respectively), the two yellow arrows point out [1 0 -1] junctions.

 

Double cross-slip (sometimes associated with junctions) have been identified in this crystal.

 

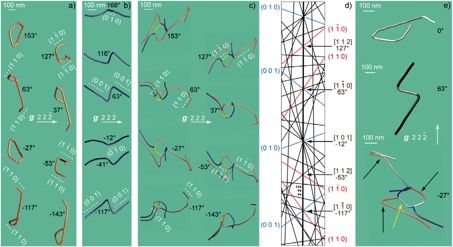
Figure 2: Double cross-slip mechanism: (a) Reconstructed volume of a [0 0 1] dislocation obtained with g = 2 2 -2 (projected angle of −143°, −117°, −53°, −27°, 37°, 63°, 127° and 153°), the (1 1 0) planes are edge-on for the −117° and 63° tilt angles ([1 -1 0] zone axis) and the (1 -1 0) planes are edge-on for the −53° and 127° tilt angles ([1 1 2] zone axis); (b) Reconstructed volume of a [1 0 0] dislocation performed with the same diffraction vector as (a) (projected angle of −117°, −41°, −12°, 63°, 116° and 168°), the (0 0 1) planes are edge-on for the −117° and 63° tilt angles and the (0 1 0) planes are edge-on for the −12° and 168° tilt angles ([1 0 1] zone axis); (c) Complex dislocation configuration composed of a [1 0 0] and a [0 0 1] dislocation, a [1 0 -1] junction (yellow segment) and an attractive [0 0 1]/[1 0 0] dislocation crossed state; moreover a double cross-slip configuration of the [0 0 1] dislocation is revealed (same description as (a)); (d) Simulation of the Kikuchi lines, between −165° and 180°, in kinematic conditions; the (0 1 0) and (0 0 1) Kikuchi lines are shown in blue colour (in reference with the [1 0 0] dislocation in blue colour) and the (1 1 0) and (1 -1 0) Kikuchi lines are shown in red colour (in reference with the [0 0 1] dislocation in orange colour); (e) Summary of the three dislocation configurations in (a), (b) and (c) for tilt angles of 0°, 63° and −27°, respectively (the white dislocations segments designate the [0 0 1](1 1 0) slip systems, the light grey dislocations segments refer to the [0 0 1](1 -1 0) slip systems and the black dislocation segments designate the [1 0 0](0 0 1) slip systems), the yellow arrow points out a [1 0 -1] junction.

 

It is the first time that a quantitative study of climb systems has been performed thanks to electron tomography.

 

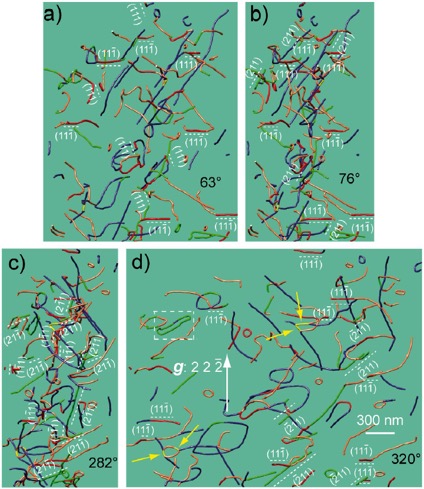
Figure 3: Dislocation climb planes (the dislocation segments which lie on the 1 planes are coloured in red and the dislocation segments are coloured in green for the 2 planes): (a) 3D reconstruction of a PoEM8 tilted series obtained with g = 2 2 -2, with a projected angle of 63° (the (1 1 -1) and (1 1 1) planes are edge-on with this projection condition); (b) Projection angle of 76° (the (1 1 -1) and (2 1 1) planes are edge-on along this direction); (c) 282° tilt angle (the (1 1 -1), (1 -1 1), (2 1 -1) and (2 -1 1) planes are edge-on with this orientation); (d) Projection angle of 320° (the (1 1 -1) and (-2 1 1) planes are edge-on with this projection condition), the white dashed square points out a break-up of a dislocation dipole by climb, the four yellow arrows point out [1 0 -1] junctions; The numerous dislocation segments which lie on the 1 and the 2 planes (19 segments in 1 and 23 segments in 2) show the occurrence of climb in PoEM8.

 

Finally, these interactions and mechanisms explain the strain hardening observed in the stress/strain compression curves of the crystal.

 

See the paper just published by our group:

A. Mussi, P. Cordier, S. Demouchy, B. Hue, "Hardening mechanisms in olivine single crystal deformed at 1090 °C: an electron tomography study". Philosophical Magazine (2017), doi:10.1080/14786435.2017.1367858